SITCOMTN-042: Image quality contribution from uncorrected quasistatic wavefront errors

• Eske Pedersen (he/him)

Latest Revision: 2022-10-27

Note

This technote is a work-in-progress.

1 Abstract

Determine image quality contribution from uncorrected quasistatic wavefront errors via donut pair

Inspired by the derivations outlined in [1], we have developed a new method for estimating uncorrected wavefront errors in the images of Auxtel. To do this requires two sets of donuts, a set taken intra-focal and a set taken extra-focal. To test our mehtod we used data from the October 2022 Auxtel run specifically we used images seq_num 578-588. These images were taken for this analysis especially, they were made with intentionally displacing focus 7.5mm on either side of focus.

2 background

Starting from with the derivation in [1]. Let us start by defining the wavefront signal \(S\):

\[S = -\frac{1}{I_0}\frac{\partial I}{\partial z} \approx -\frac{1}{\Delta z}\frac{I_1 -I_2}{I_1 + I_2}.\]

Where the focus offset \(\Delta z\) in object space is given by:

\[\Delta z = f(f-\ell)/\ell\]

Where \(f\) is the focal length and \(\ell\) is the defocus distance, that is how far from focus the two images \(I_1\) and \(I_2\) are taken from focus. One image taken intra-focal and the other extra-focal.

It turns out we can approximate the Laplacian of the wavefront error as:

\[\nabla^2 W \approx S\]

From this we get the idea that we can get the tilt of the wavefront as the integral of the S with respect to \(x\) and \(y\) in the pupil frame:

\[\begin{split}T_x(x,y) = \int_{-R_x}^x S(x',y) dx'\\ T_y(x,y) = \int_{-R_y}^y S(x,y') dy'\end{split}\]

Where \(R_{x/y}\) is the radius of the donut, with our cordinate system centered on the donut center. This corresponds to taking the cummulative sum in the \(x\) and \(y\) directions. Adding these in Quadrature we obtain an estimate for the Pixel tilt:

\[T_\text{pixel} = \sqrt{T_x^2+T_y^2}\]

Finally we can from the Pixel tilt obtain the RMS of the this tilt, which should correspond to the RMS of the residual wavefront error.

Warning

We are currently having an issue where there seems to be a factor 2 difference between the RMS from tilt and the theoretical RMS for the wavefront error.

3 Data processing:

We processed the donuts by first isolating the each of the 11 donuts. To do this we find the center of each donut utilizing the same methods as utilized in :cite:p:’sitcom-27’. Once each donut has been isolated and we found centers for them, we average over the 5 donuts we have at each position. We make cut-outs around each donut, utilizing the center of the donut and the finding the largest radius of the donuts. Next we take the averages of the images on either side of focus, followed by a masking of the donuts. We utilized two different masking techniques, first we made circular masks using the information obtained about the circles of the donut to generate and artificial donut mask that fit with the average donut image. The second method we instead utilize the masking used in :cite:p:’sitcom-27’ to generate the masks. The advantage of the second method is that we get the spiders in the donuts cut out. After having masked the averages on either side of the focus, we the process them as indicated in the background section.

4 Simulations:

As a sanity check of the method we conducted our analysis on both real data and on a set of simulated donuts. We generated the donuts using Josh Myers’ Donut generating code Danish, which is based on his batoid code Batoid.

We generated donuts with a set of configurations that should correspond to the Auxtel setup. We analysed a set that was displaced \(0.75mm\) from focus.

5 Results:

From the data processing we obtain the follwing results, dependent on our masking.

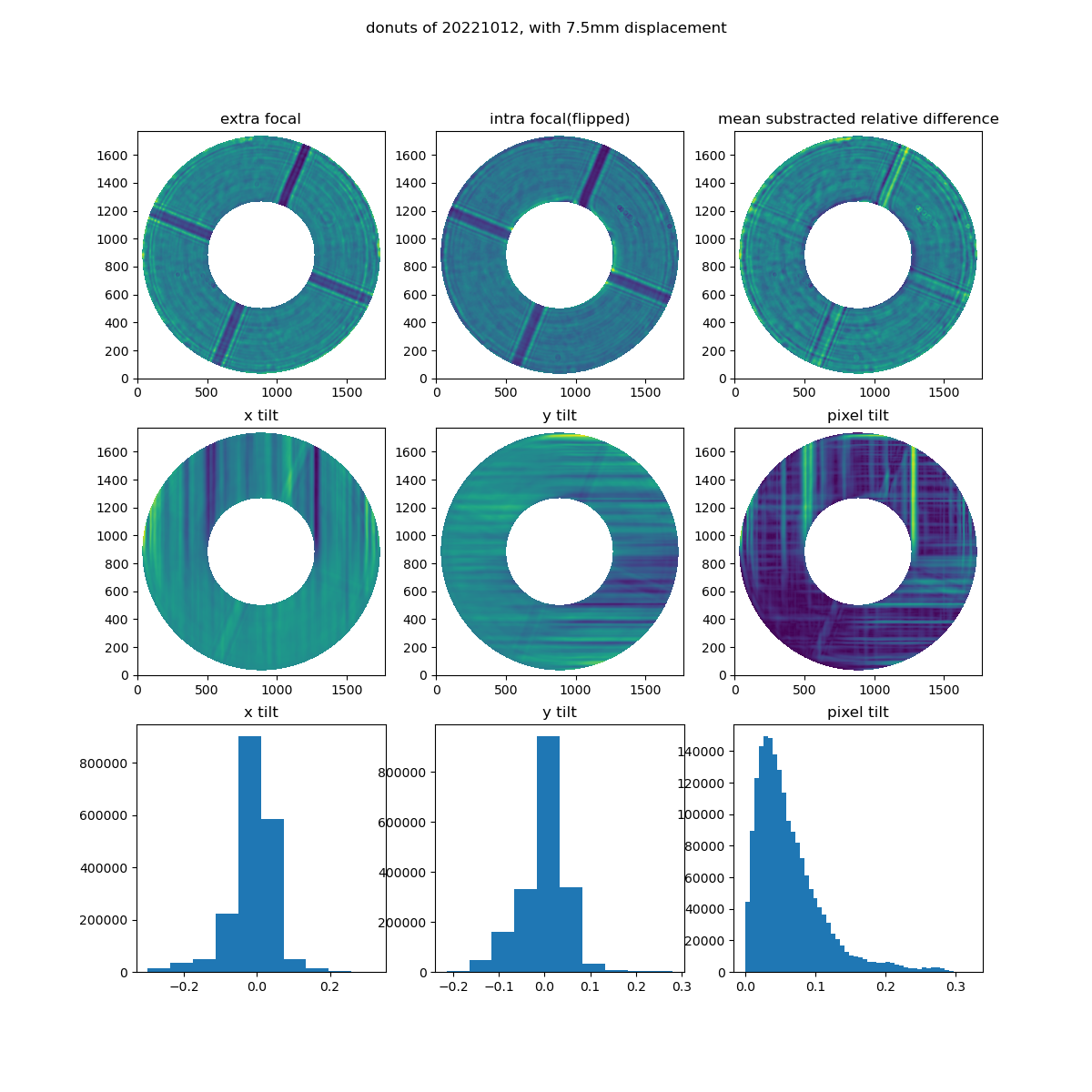
Figure 1 We see here the results utilizing the simple circular mask to include all of the donut, but not cutting out the spiders.

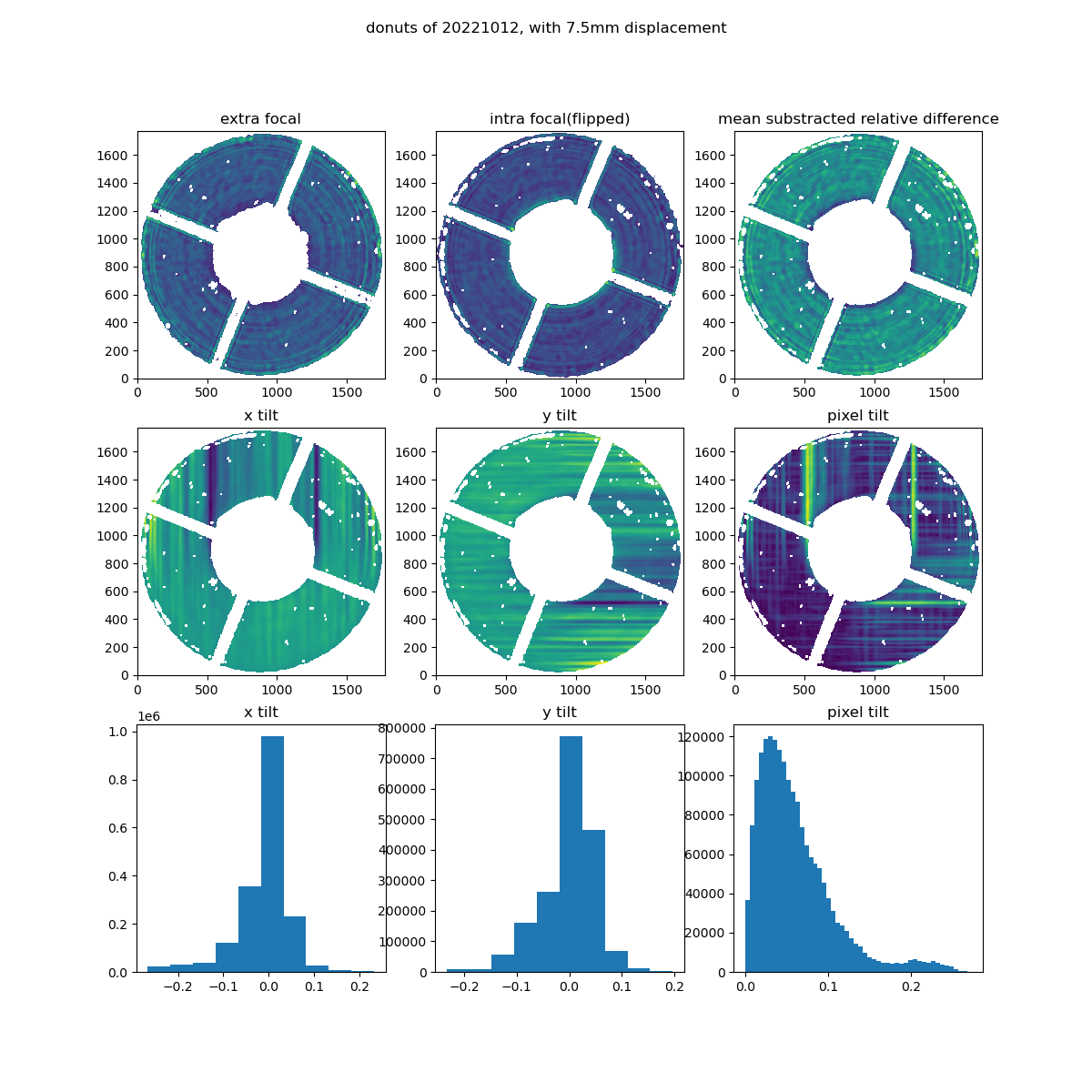
Figure 2 Here we utilized the more advanced mask, it cuts out parts of the donut that fall below a certain cutting value, but it has the advantage that it also cuts out the spiders in the donuts

Once we have obtained the tilts we can then estimate the RMS of the pixel tilt:

We obtain for the simple mask: 0.077264264

While for the advanced mask we obtain: 0.07585939

So we see very little difference. we also see that the uncorrected wavefront error is of the order \(10^{-2}\) arcsecs.

[1] (1,2)

Bo Xin, Chuck Claver, Ming Liang, Srinivasan Chand rasekharan, George Angeli, and Ian Shipsey. Curvature wavefront sensing for the large synoptic survey telescope. \ao , 54(30):9045, Oct 2015. arXiv:1506.04839, doi:10.1364/AO.54.009045.